深度学习系列(二)：全连接神经网络和BP算法

发表于2022-01-01更新于2023-04-25字数统计3.1k阅读时长17分阅读次数

前言

上篇介绍了深度学习框架pytorch的安装以及神经网络的基本单元：感知机。本文将介绍全连接神经网络(FCNet)的结构和训练方法，全连接神经网络是一种典型的前馈网络。感知机解决不了非线性分类问题，但是多层神经元叠加在一起理论上可以拟合任意的非线性连续函数映射。

全连接网络

全连接网络是一种前馈网络，由输入层、输出层和若干个隐层组成。如下图所示，输入层由dd个神经元组成，用于输入样本的各个特征值；网络可以存在若干个隐层，每个隐层的神经元个数也是不确定的；输出层由ll个神经元组成，ll就是最后要分类的类别数。因此神经网络由很多层构成。

神经元之间的连接方式为：同一层之间的神经元没有连接关系，每一层的神经元和下一层的所有神经元连接。每两个连接的神经元之间都有一个连接权重，这里记第ii个神经元和下一层第jj个神经元的权重为ωij\omega_{ij}。
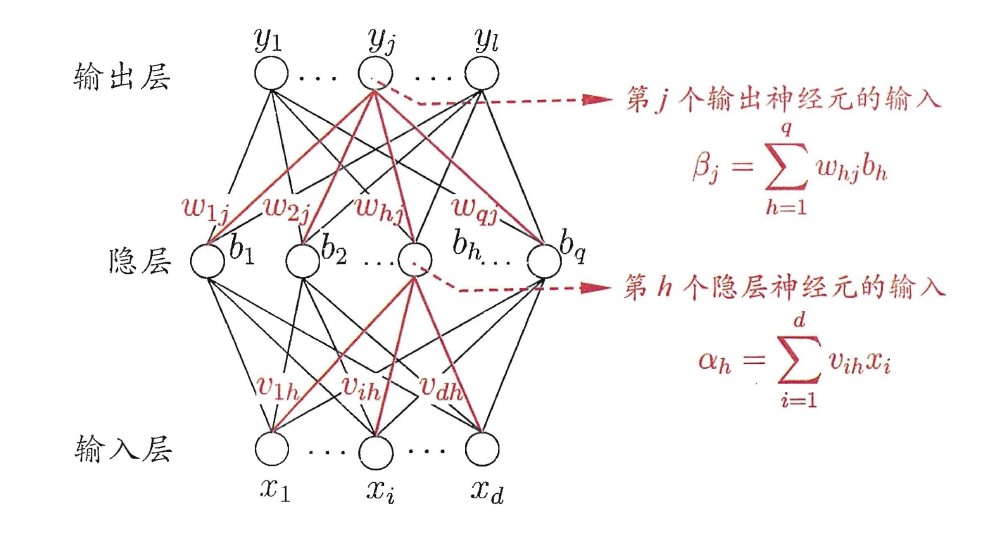
全连接神经网络
以上图中只有一个隐层的神经网络为例，隐层的第hh个神经元的输入可以表示为：

αh=∑i=1dvihxi\alpha_h = \sum_{i=1}^d v_{ih}x_i

其输出则是输入经过激活函数ff作用在输入上，这里取激活函数为Sigmoid函数：

sigmoid(x)=11+e−xsigmoid(x) = \frac{1}{1+e^{-x} }

之前我们使用的是阶跃函数，Sigmoid也是一个非线性函数，它有一个很好的性质就是它的导数可以用自己本身来表示：

y′=y(1−y)y'=y(1-y)

阶跃函数和Sigmoid的函数图如下：
激活函数
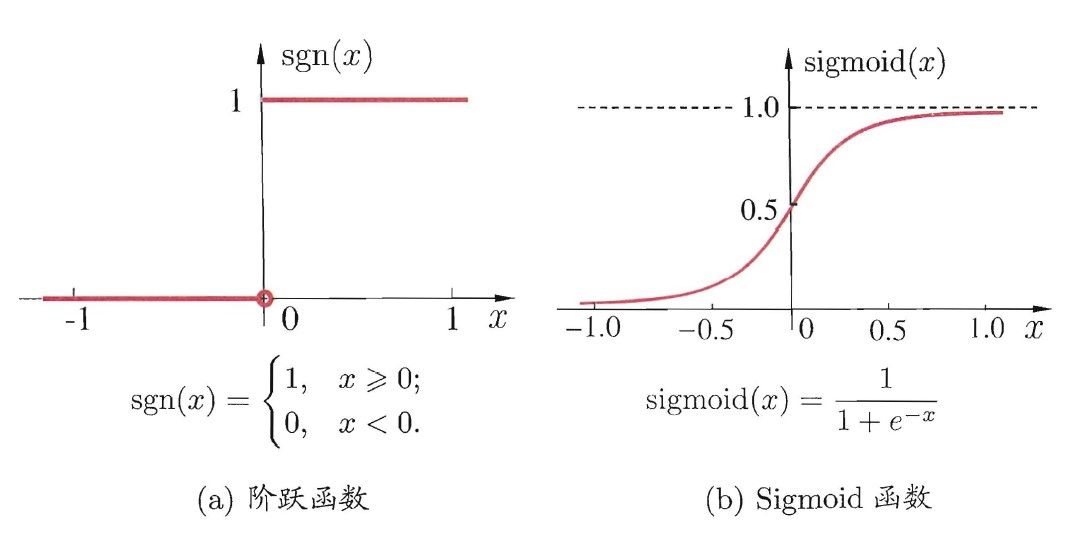
这样全连接网络的输出计算也就是前向传播的过程为：首先通过输入层计算得到第一个隐层的输出，第ii个神经元至第hh个神经元的计算公式为：

output=f(∑i=1dvihxi)output = f( \sum_{i=1}^d v_{ih}x_i)

然后通过第一个隐层计算下一个隐层的值，最后传播到输出层，最后得到神经网络的输出为：

y^=(y^1,y^2,...,y^l)\mathbf {\hat y}=(\hat y_1, \hat y_2, ... ,\hat y_l)

神经网络训练之BP算法

我们知道神经网络之所以能够具有很好的拟合能力，就是因为多个神经元之间的连接权重在起作用，那么对上面介绍的神经网络应该怎么训练呢？应该怎么找到最适合一个数据集分类的各个神经元之间连接的权重ωij\omega_{ij}呢？反向传播算法（Back Propagation)提供了解决方法。

训练的思路同样是梯度下降算法，我们定义一个损失函数LL，通过朝着损失函数下降最快的方向也就是梯度方向去调整我们的权重系数。损失函数可以为均方误差：

E=12∑j=1m(y^j−yj)2E=\frac{1}{2} \sum_{j=1}^m (\hat y_j - y_j)^2

接下来的问题就是求损失函数EE对需要训练的权重系数的梯度∂E∂ωij\frac {\partial E}{\partial \omega_{ij} }。

输出层权重训练

首先以从隐层至输出层的连接权重ωhj\omega _{hj}为例进行推导。这个求梯度的过程就是链式求导法则，首先我们分析一下ωhj\omega_ {hj}是如何影响到我们的损失函数EE的，ωhj\omega_ {hj}首先影响了第jj个输出层神经元的输入值βj\beta_j，然后进而通过激励函数Sigmoid影响到其输出值y^j\hat y_j，然后影响到EE。
这个求导过程为：

∂E∂ωhj=∂E∂y^j×∂y^j∂βj×∂βj∂ωhj\frac {\partial E}{\partial \omega_{hj} } = \frac {\partial E}{\partial {\hat y_j} } \times \frac{\partial {\hat y_j} }{\partial \beta_j} \times \frac{\partial \beta_j}{\partial \omega_{hj} }

我们分别来分析这三项：

第一项：
将上面EE的表达式代入∂E∂y^j\frac {\partial E}{\partial {\hat y_j} }：

∂E∂y^j=∂∂y^j12∑j=1m(y^j−yj)2=−(yj−y^j)\frac {\partial E}{\partial {\hat y_j} } = \frac{\partial}{\partial {\hat y_j} } \frac{1}{2} \sum_{j=1}^m (\hat y_j - y_j)^2 = -(y_j - \hat y_j)

第二项：
这一项是神经元输出对输入求导，实际上就是Sigmoid求导：

∂y^j∂βj=yj(1−yj)\frac{\partial {\hat y_j} }{\partial \beta_j} = y_j(1-y_j)

第三项：
这一项是神经元的输入对权重求导，实际上就等于上一个神经元的值bhb_h:

∂βj∂ωhj=bh\frac{\partial \beta_j}{\partial \omega_{hj} } = b_h

所以根据梯度下降规则更新权重过程为：

ωhj←ωhj−η∂E∂ωhj\omega_{hj} \gets \omega_{hj} - \eta \frac {\partial E}{\partial \omega_{hj} }

=ωji+η(yj−y^j)yj(1−yj)bh=ηδjbh=\omega_ji + \eta (y_j - \hat y_j) y_j(1-y_j) b_h = \eta \delta_j b_h

上式中的δj\delta_j我们定义为：

δj=(yj−y^j)yj(1−yj)\delta_j = (y_j - \hat y_j) y_j(1-y_j)

隐层权重训练

隐层神经元权系数vihv_{ih}首先影响bhb_h神经元的输入αh\alpha_h，进而影响输出。

∂E∂vih=∂E∂bh×∂bh∂αh×∂αh∂vih=∑j=1l∂E∂βj×∂βj∂bh×bh(1−bh)×xi\frac{\partial E}{\partial{v_{ih} } } = \frac{\partial E}{\partial b_h} \times \frac{\partial b_h}{\partial \alpha_h} \times \frac{\partial \alpha_h}{\partial v_{ih} } = \sum_{j=1}^l \frac{\partial E}{\partial \beta_j} \times \frac{\partial \beta_j}{\partial b_h} \times b_h(1-b_h) \times x_i

=xibh(1−bh)∑j=1lωhjδj=x_i b_h(1-b_h) \sum_{j=1}^l \omega_{hj} \delta_j

至此，我们求出了损失函数对输出层权重系数的梯度和对隐层权重系数的梯度，然后就可以根据梯度下降算法对我们的网络进行训练了。

反向传播算法原理比较简单，推导起来由于标号复杂显得繁琐，后面我们训练网络不怎么关心反向传播的内部求解过程，因为pytorch提供了自动求导的功能，这一点让使用者着重于自己的网络结构构建和参数调节，十分方便！！

花这么大功夫敲公式推导BP算法只是为了让读者对训练的过程有个清楚的理解，接下来在pytorch中实战一个简单的全连接网络。

Pytorch 全连接网络实现

Pytorch 上手非常容易，这里有个翻译版的60min入门：
https://www.jianshu.com/p/889dbc684622
使用的数据集为Mnist手写数字，训练集有60000个样本，测试集有10000个样本，首先我们建立一个工程并下载数据集如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
import torch
from torchvision import datasets, transforms

if __name__ == '__main__':
    # Pytorch自带Mnist数据集，可以直接下载，分为测试集和训练集
    train_dataset = datasets.MNIST(root='./data/', train=True, transform=transforms.ToTensor(), download=True)
    test_dataset = datasets.MNIST(root='./data/', train=False, transform=transforms.ToTensor(), download=True)
    # DataLoader类可以实现数据集的分批和打乱等
    train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=16, shuffle=False)
    test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=16, shuffle=False)
    for i, data in enumerate(train_loader, 0):
        image, label = data
        print(image.shape)

torch里面有MNIST数据集，所以直接调用datasets.MNIST下载就行了，然后将得到的数据集用DataLoader类装起来，这个对象参数中的batch_size为每一批的样本个数，也就是训练时一次性装载进内存的数据，shuffle是将数据集顺序打乱的操作。

这段代码的运行输出：
输出
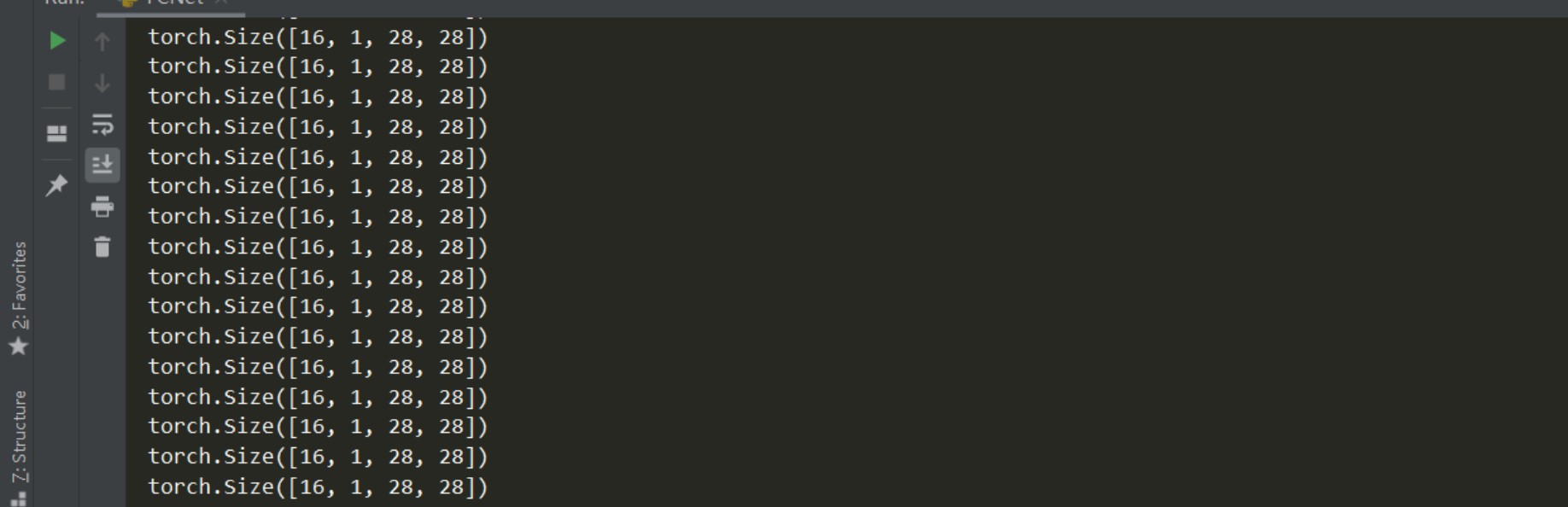
可以看到打印出的Tensor是四维的一个数组，以后我们输入神经网络的都是一个四维的Tensor，第一维为batch_size，后面三维为图像的C*W*H，也就是颜色通道数和图像的长宽。MNIST是黑白的数据集，所以颜色通道为1，对于彩色图片来说通道数为3。

装载完数据就可以进行神经网络的构建了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
import torch
import torch.nn as nn
from torch.optim import optimizer
from torchvision import datasets, transforms

# 优先选择gpu
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")


class FCNet(nn.Module):
    def __init__(self):
        super(FCNet, self).__init__()
        # 一共三层神经网络，一个隐层
        self.features = nn.Sequential(
            nn.Linear(784, 100),
            nn.Sigmoid(),
            nn.Linear(100, 10)
        )

    # 前向传播
    def forward(self, x):
        # 输入为16*1*28*28，这里转换为16*784
        x = x.view(16, -1)
        output = self.features(x)
        return output


# 训练网络
def train(train_loader):
    # 损失函数值
    running_loss = 0.0
    for i, data in enumerate(train_loader, 0):
        inputs, labels = data
        # 如果有gpu，则使用gpu
        inputs, labels = inputs.to(device), labels.to(device)

        # 梯度置零
        optimizer.zero_grad()
        # 前向传播
        output = net(inputs)
        # 损失函数
        loss = criterion(output, labels)
        # 反向传播，权值更新
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        # 每50个batch_size后打印一次损失函数值
        if i % 100 == 99:
            print('%5d loss: %.3f' %
                (i + 1, running_loss / 100))
            running_loss = 0.0


# 训练完1个或几个epoch之后，在测试集上测试以下准确率，防止过拟合
def test(test_loader):
    correct = 0
    total = 0
    # 不进行autograd
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)
            outputs = net(images)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()

    print('Accuracy of the network on test images: %d %%' % (
            100 * correct / total))
    return correct / total


if __name__ == '__main__':
    # Pytorch自带Mnist数据集，可以直接下载，分为测试集和训练集
    train_dataset = datasets.MNIST(root='./data/', train=True, transform=transforms.ToTensor(), download=True)
    test_dataset = datasets.MNIST(root='./data/', train=False, transform=transforms.ToTensor(), download=True)
    # DataLoader类可以实现数据集的分批和打乱等
    train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=16, shuffle=False)
    test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=16, shuffle=False)

    net = FCNet().to(device)
    # 准则函数使用交叉熵函数，可以尝试其他
    criterion = nn.CrossEntropyLoss()
    # 优化方法为带动量的随机梯度下降
    optimizer = torch.optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

    for epoch in range(20):
        print('Start training: epoch {}'.format(epoch+1))
        train(train_loader)
        test(test_loader)

不熟悉pytorch建议先看看上面的教程，上手很快，这个框架也给了我们很多便利，搭建神经网络十分简单。

上述代码搭建的是一个最简单的三层的全连接网络，输入层神经元为28*28也就是每张图的像素个数，有一个隐层为100个神经元，输出层为10个神经元对应10类数字。代码注释比较详细，这里不细说。

最后训练的结果：
训练结果
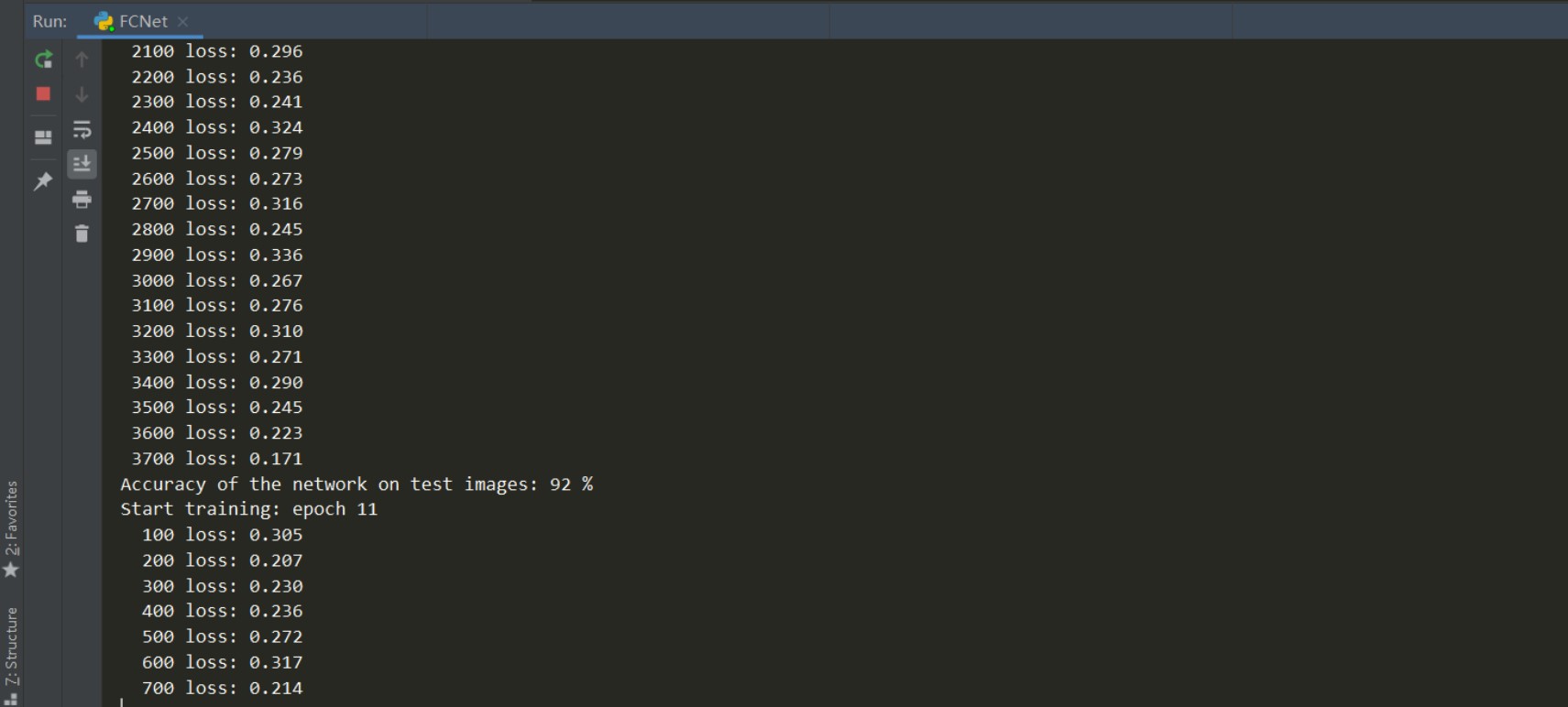
这里可以看到，经过10轮的训练之后，网络对测试集的准确率达到了0.92，这还仅仅是一个最简单的三层全连接网络！可见神经网络的强大。

这里要注意的就是，网络的训练都是前几轮损失函数值下降的很快，准确率上升也快，后面损失函数就不怎么下降了，这也意味着我们的模型正在逐渐收敛。由于网络简单且图片较小，网络的训练很快，特别是使用GPU的话。

我这里20轮训练之后，准确率达到了94%，但是一直训练下去的话会发现网络准确率不再上升，这是因为网络的结构本身比较简单，学习能力有限，之后我们会使用卷积神经网络对这个数据集进行分类，能够达到更高的准确率。

总结

本篇文章主要介绍了全连接神经网络的基本结构以及著名的反向传播算法（BP）的原理推导，最后使用pytorch实现了一个最简单的全连接神经网络对MNIST手写数据集进行分类，实例中的代码已经上传至github：https://github.com/Fanxiaodon/nn/tree/master/FCNetMnist
全连接神经网络存在一些缺陷，后面我们会提到，下篇介绍卷积神经网络CNN，CNN相比全连接网络有一些较大的优点，广泛应用于图像处理。

参考资料

  1. 周志华《机器学习》
  2. PyTorch 深度学习: 60分钟快速入门