卡尔曼滤波理论推导

发表于2022-04-26更新于2023-12-03字数统计3.8k阅读时长30分阅读次数

前言

这几天学习了卡尔曼滤波器（Kalman Filter）相关的理论知识，并发现了一个非常仔细的推导过程，是在b站上发现的一个搞控制的博士DR_CAN：https://space.bilibili.com/230105574，看完他的卡尔曼滤波器相关的视频，加深了我对理论的理解，这里将视频中的推导过程加以梳理，以便日后查看。

数据融合

一个例子

首先，我们举一个简单的例子来理解一下测量中的递推，假设我们对某一物理量进行多次测量，并使用取平均值的方式来估计其真实值：

x^k=1k(z1+z2+...+zk)(1)\hat{x}_k = \frac{1}{k}(z_1+z_2+...+z_k) \tag{1}

其中 x^k\hat{x}_k 是我们对真实值的估计，ziz_i 是第 ii 次测量的测量值。我们对上式进行简单变换称为递推形式：

x^k=1k(z1+z2+...+zk)=1k(z1+z2+...+zk−1)+1kzk=k−1kx^k−1+1kzk =x^k−1+1k(zk−x^k−1)(2)\begin{aligned} \hat{x}_k &= \frac{1}{k}(z_1+z_2+...+z_k) \\ &= \frac{1}{k}(z_1+z_2+...+z_{k-1})+\frac{1}{k}z_k \\ &= \frac{k-1}{k}\hat{x}_{k-1}+\frac{1}{k}z_k\ \\ &= \hat{x}_{k-1}+\frac{1}{k}(z_k-\hat{x}_{k-1}) \tag{2} \end{aligned}

上式的含义就是我们对该物理量进行 kk 次测量之后的估计值 x^k\hat{x}_k 为第 k−1k-1 次测量后估计值 x^k−1\hat{x}_{k-1} 和后面一项的，而后面那项受到第 kk 次测量值的影响。且随着 kk 不断增大，后面项趋于 00，估计值也就不在变化了。

我们可以把式 (2) 中后一项增益改写一下：

x^k=x^k−1+Kk(zk−x^k−1)(3)\begin{aligned} \hat{x}_k = \hat{x}_{k-1}+K_k(z_k-\hat{x}_{k-1}) \tag{3} \end{aligned}

这个 KkK_k 就相当于卡尔曼滤波器中的卡尔曼增益（Kalman Gain），在后面会进行详细推导。

数据融合的例子

下面举另一个测量的例子来加深对上述增益的理解。假设还是对一个物理量进行测量，我们有两种测量传感器，且两种传感器都存在测量误差，我们假设误差服从高斯分布。其中第一种传感器测量出来的值为 z1=30z_1 = 30，它的误差标准差为 σ1=2\sigma_1=2；第二种传感器测量出来的值为 z2=32z_2 = 32，它的误差标准差为 σ1=4\sigma_1=4。现在的问题是如何找到一个最优的估计值 z^\hat{z} 来估计该物理量的真实值。

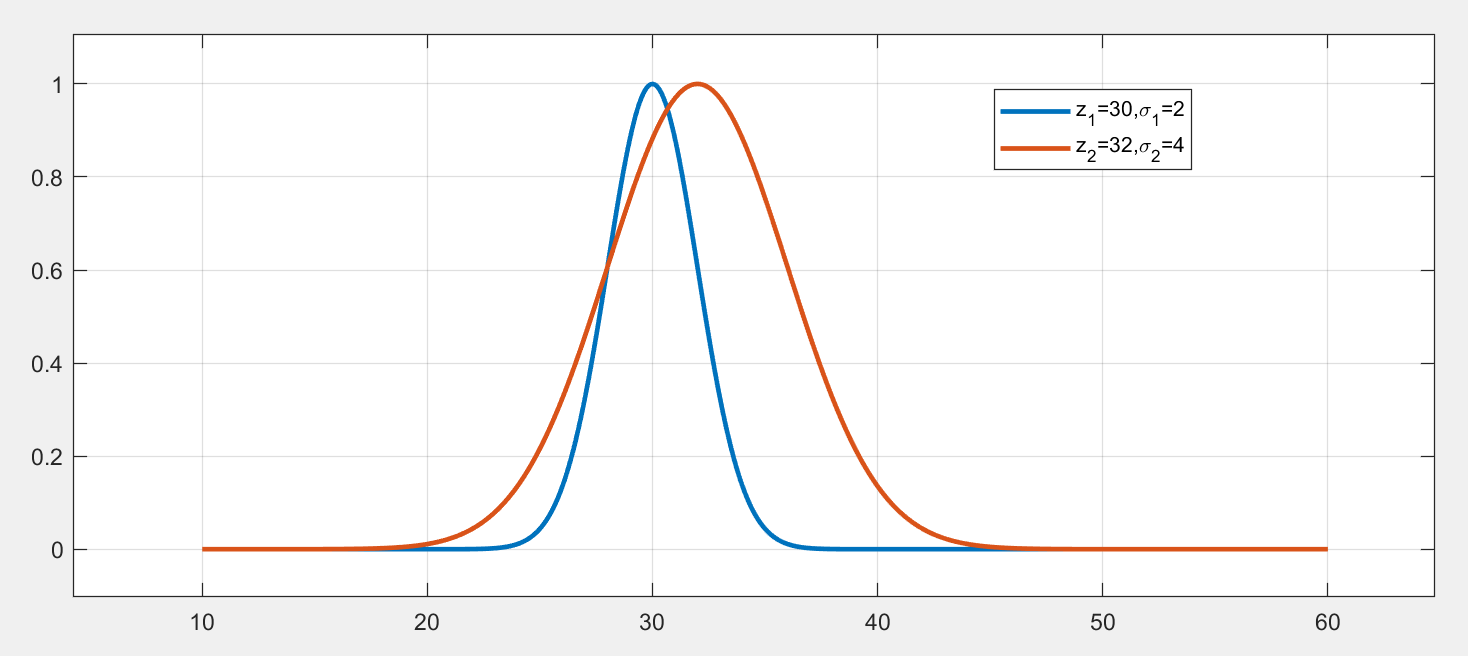
我们用上一个例子中思想进行融合，最终的测量估计值为第一个传感器的测量值和两者测量值差的加权和：

z^=z^1+K(z2−z1)(4)\begin{aligned} \hat{z} = \hat{z}_1+K(z_2-z_1) \tag{4} \end{aligned}

我们需要找到这个增益 KK 使得最终估计值的方差最小，也就是得到最优的估计值。这个方差计算如下：

σz^2=var(z1+K(z2−z1))=var((1−K)z1+Kz2)=(1−K)2var(z1)+K2var(z2)=(1−K)2σ12+K2σ22(5)\begin{aligned} \sigma_{\hat{z}}^2 &= var(z_1+K(z_2-z_1)) \\ &= var((1-K)z_1+Kz_2)\\ &= (1-K)^2var(z_1)+K^2var(z_2)\\ &= (1-K)^2\sigma_1^2+K^2\sigma_2^2\tag{5} \end{aligned}

需要使得方差最小，我们将其对 KK 求导并令其等于 0，求出相应的最小值点：

dσz^2dK=−2(1−K)σ12+2Kσ22=0K=σ12σ12+σ22(6)\begin{aligned} &\frac{d \sigma_{\hat{z}}^{2}}{d K}=-2(1-K) \sigma_{1}^{2}+2 K \sigma_{2}^{2}=0 \\ &K=\frac{\sigma_{1}^{2}}{\sigma_{1}^{2}+\sigma_{2}^{2}}\tag{6} \end{aligned}

带入上面的测量值和方差可以求出：K=0.2K=0.2，σz^2=3.2\sigma_{\hat{z}}^{2}=3.2，z^=30.4\hat{z}=30.4。最终的融合结果如下图：

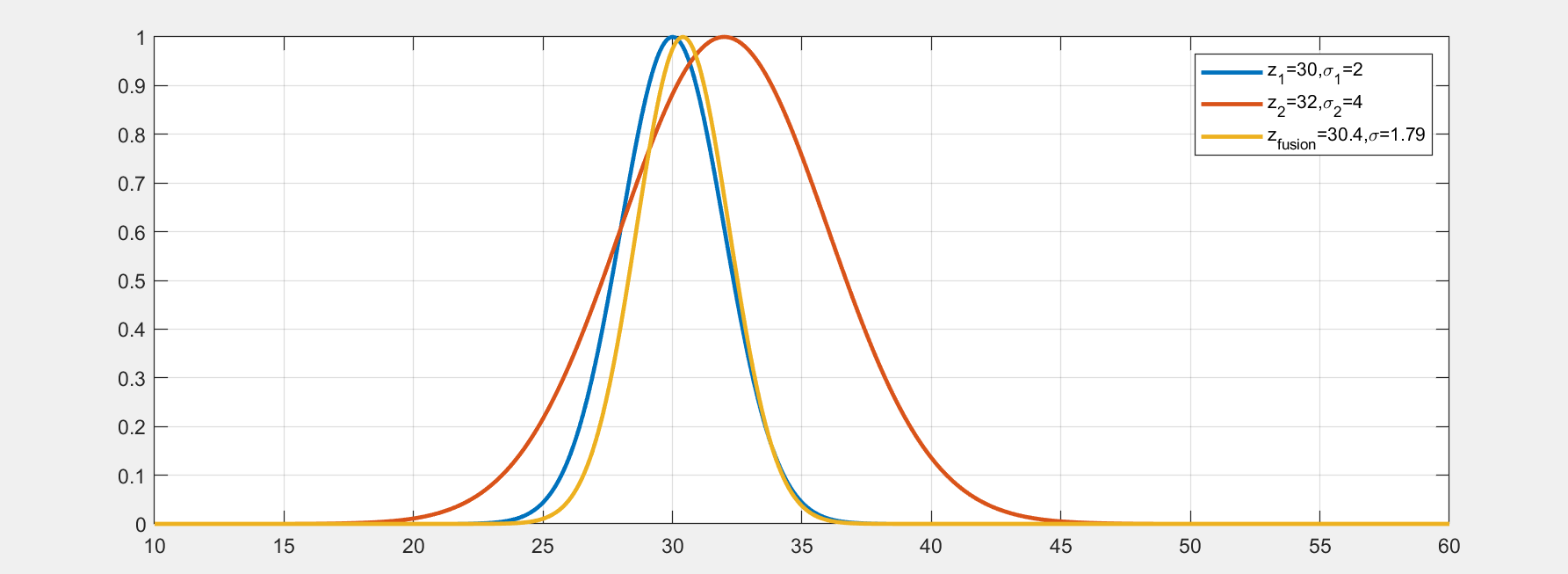
卡尔曼增益

我们使用离散状态空间方程描述一个系统：

xk=Axk−1+Buk−1+wk−1zk=Hxk+vk(7)\begin{aligned} &x_{k}=A x_{k-1}+B u_{k-1}+w_{k-1} \\ &z_{k}=H x_{k}+v_{k}\tag{7} \end{aligned}

其中，wk−1w_{k-1} 是过程噪声，假设其服从高斯分布：p(w)∼(0,Q)p(w) \sim (0, Q)，其中 QQ 为过程噪声的协方差矩阵；同样 vkv_{k} 为测量噪声，假设也服从高斯分布：p(v)∼(0,R)p(v) \sim (0, R)，RR 为测量噪声的协方差矩阵。

在实际过程中，我们估计状态真实值时，无法知道过程噪声，于是我们的通过模型估计出的状态值（这里称为先验估计值）x^k−\hat{x}_{k}^{-} 为：

x^k−=Ax^k−1+Buk−1(8)\begin{aligned} \hat{x}_{k}^{-}=A \hat{x}_{k-1}+B u_{k-1}\tag{8} \end{aligned}

同样，我们也无法知道测量噪声，于是我们通过测量得到的估计值 x^kmea\hat{x}_{kmea}为：

x^kmea =H−zk(9)\begin{aligned} \hat{x}_{\text {kmea }}=H^{-} z_{k}\tag{9} \end{aligned}

这里同样使用上面数据融合的思想，将两种估计值进行加权融合得到最终的估计值 x^k\hat{x}_k：

x^k=x^k−+G(H−zk−x^k−)(10)\begin{aligned} \hat{x}_{k}=\hat{x}_{k}^{-}+G\left(H^{-} z_{k}-\hat{x}_{k}^{-}\right)\tag{10} \end{aligned}

上式中的 GG 为加权的增益参数,其范围为 [0,1][0,1]，当 GG 越接近于 00 时，最终的估计值更接近于模型算出来的先验估计值；当 GG 越接近于 11 时，最终的估计值更接近于传感器测量出来的值。

对上式进行简单的变形（把增益区间变为了 [0,H−][0,H^{-}]），令 G=KkHG=K_kH，上式变为：

x^k=x^k−+Kk(zk−Hx^k−)(11)\begin{aligned} \hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(z_{k}-H \hat{x}_{k}^{-}\right)\tag{11} \end{aligned}

和前文中数据融合中一样，我们现在的目标变为：如何找到一个增益 KkK_k 使得最终的估计值最接近真实值。

不难想到，这个增益的取值和模型中的过程噪声 wk−1w_{k-1} 以及测量噪声 vkv_{k} 有关系，当测量噪声很大时，我们希望最终的估计值更多的依赖于模型计算值（先验估计值），此时希望增益 KkK_k 很小；当模型中的过程噪声很大时，我们希望最终的估计值更多的依赖于传感器的测量值，此时希望增益 KkK_k 很大。

我们使用 eke_k 来衡量真实值和估计值之间的误差：

ek=xk−x^k(12)\begin{aligned} e_k=x_k-\hat{x}_k\tag{12} \end{aligned}

这个 eke_k 也是服从均值为 00 的高斯分布的：p(ek)∼(0,P)p(e_k) \sim (0,P)，这里的 PP 为其协方差矩阵，它的值可以这样计算：P=E[ee⊤]P=E[ee^\top]，也就是ee⊤ee^\top的期望。且这个协方差矩阵的对角线元素为各个误差分量 eie_i 的方差（读者不妨令 ee为二阶列向量 [e1,e2]⊤[e_1, e_2]^\top 进行验证），我们需要使最终误差最小，也就是使其协方差矩阵的迹 tr(P)tr(P) 最小。

我们首先计算协方差矩阵 PP ：

P=E[ee⊤]=E[(xk−x^k)(xk−x^k)⊤](13)\begin{aligned} P &=E\left[e e^{\top}\right] \\ &=E\left[\left(x_{k}-\hat{x}_{k}\right)\left(x_{k}-\hat{x}_{k}\right)^{\top}\right]\tag{13} \end{aligned}

由式（11），我们知道：

xk−x^k=xk−(x^k−+Kk(zk−Hx^k−))=xk−x^k−−Kk(Hxk+vk)+KkHx^k−=xk−x^k−−KkH(xk−x^k−)−Kkvk=(I−KkH)(xk−x^k−)−Kkvk(14)\begin{aligned} x_{k}-\hat{x}_{k} &=x_{k}-\left(\hat{x}_{k}^{-}+K_{k}\left(z_{k}-H \hat{x}_{k}^{-}\right)\right) \\ &=x_{k}-\hat{x}_{k}^{-}-K_{k}\left(H x_{k}+v_{k}\right)+K_{k} H \hat{x}_{k}^{-} \\ &=x_{k}-\hat{x}_{k}^{-}-K_{k} H\left(x_{k}-\hat{x}_{k}^{-}\right)-K_{k} v_{k} \\ &=\left(I-K_{k} H\right)\left(x_{k}-\hat{x}_{k}^{-}\right)-K_{k} v_{k}\tag{14} \end{aligned}

我们记上式中的 xk−x^k−x_{k}-\hat{x}_{k}^{-} 为先验误差ek−e_k^{-}，并将式（14）代入（13），有：

Pk=E[(I−KkH)ek−−Kkvk][ek−⊤(I−KkH)⊤−vk⊤Kk⊤]=E(I−KkH)ek−ek−⊤(I−KkH)⊤−E(I−KkH)ek−vk⊤Kk⊤−EKkvkek−⊤(I−KkH)⊤+EKkvkvk⊤Kk⊤=(I−KkH)E(ek−ek−⊤)(I−KkH)⊤+KkE(vkvk⊤)Kk⊤(15)\begin{aligned} P_k&=E[\left.\left(I-K_{k} H\right) e_{k}^{-}-K_{k} v_{k}\right]\left[e_{k}^{-\top}\left(I-K_{k} H\right)^{\top}-v_{k}^{\top} K_{k}^{\top}\right] \\ &=E\left(I-K_{k} H\right) e_{k}^{-} e_{k}^{-\top}\left(I-K_{k} H\right)^{\top}-E\left(I-K_{k} H\right) e_{k}^{-} v_{k}^{\top} K_{k}^{\top} -E K_{k} v_{k} e_{k}^{-\top}\left(I-K_{k} H\right)^{\top}+E K_{k} v_{k} v_{k}^{\top} K_{k}^{\top} \\ &=\left(I-K_{k} H\right) E\left(e_{k}^{-} e_{k}^{-\top}\right)\left(I-K_{k} H\right)^{\top}+K_{k} E\left(v_{k} v_{k}^{\top}\right) K_{k}^{\top} \tag{15} \end{aligned}

上面四项中中间两项为 0，这是因为 ek−e_k^{-} 和 vk⊤v_k^{\top}相互独立，且它们期望为0。在上面的式（15）中我们记 E(ek−ek−⊤)E\left(e_{k}^{-} e_{k}^{-\top}\right) 为 Pk−P_k^{-}，称为先验协方差矩阵；E(vkvk⊤)E\left(v_{k} v_{k}^{\top}\right) 又等于系统测量噪声的协方差矩阵 RR 。

所以式（15）进一步写成：

Pk=(I−KkH)Pk−(I−KkH)⊤+KkRKk⊤=Pk−−KkHPk−−Pk−H⊤Kk⊤+KkHPk−H⊤Kk⊤+KkRKk⊤(16)\begin{aligned} P_{k}&=\left(I-K_{k} H\right) P_{k}^{-}\left(I-K_{k} H\right)^{\top}+K_{k} R K_{k}^{\top} \\ &=P_{k}^{-}-K_{k} H P_{k}^{-}-P_{k}^{-} H^{\top} K_{k}^{\top}+K_{k} H P_{k}^{-} H^{\top} K_{k}^{\top}+K_{k} R K_{k}^{\top}\tag{16} \end{aligned}

别忘了我们的目的是求出使 tr⁡(Pk)\operatorname{tr}(P_{k}) 最小的 KkK_k，注意到上式第二项和第三项互为转置(Pk−P_{k}^{-} 为对称矩阵)，因而：

tr⁡(Pk)=tr⁡(Pk−)−2tr⁡(KkHPk−)+tr⁡(KkHPk−H⊤Kk⊤)+tr⁡(KkRKk⊤)(17)\begin{aligned} \operatorname{tr}\left(P_{k}\right)=\operatorname{tr}\left(P_{k}^{-}\right)-2 \operatorname{tr}\left(K_{k} H P_{k}^{-}\right)+\operatorname{tr}\left(K_{k} H P_{k}^{-} H^{\top} K_{k}^{\top}\right)+\operatorname{tr}\left(K_{k} R K_{k}^{\top}\right)\tag{17} \end{aligned}

将上式（17）对 KkK_k 求导，并求出极值点：

dtr⁡(Pk)dkk=−2(HPk−)⊤+2KkHPk−H⊤+2KkR=0(18)\begin{aligned} \frac{d \operatorname{tr}\left(P_{k}\right)}{d k_{k}}=-2\left(H P_{k}^{-}\right)^{\top}+2 K_{k} H P_{k}^{-} H^{\top}+2 K_{k} R=0\tag{18} \end{aligned}

可以得到：

Kk=Pk−H⊤HPk−H⊤+R(19)\begin{aligned} K_{k}=\frac{P_{k}^{-} H^{\top}}{H P_{k}^{-} H^{\top}+R}\tag{19} \end{aligned}

上式（19）就是卡尔曼滤波器中最重要的公式，卡尔曼增益的求法。实际上，从上式我们也能看出来卡尔曼增益和测量误差之间的简单关系，当测量误差很大（RR很大）时，卡尔曼增益 KkK_k 趋近于 00，由式（11）最终估计值由模型先验值决定；当测量误差很小（RR很小）时，卡尔曼增益 KkK_k 趋近于 H−H^{-}，最终估计值由测量值决定。

至此，卡尔曼增益就推导完毕了。

卡尔曼滤波器

推导完卡尔曼增益之后，我们来看整个卡尔曼滤波器如何工作。

实际上，式（19）中的 Pk−P_k^{-} 我们还没有推导如何计算得到，我们根据上面的约定有：

Pk−=E[ekek−⊤](20)\begin{aligned} P_{k}^{-}=E\left[e_{k} e_{k}^{-\top}\right]\tag{20} \end{aligned}

而：

ek−=xk−x^k−=Axk−1+Buk−1+wk−1−Ax^k−1−Buk−1=A(xk−1−x^k−1)+wk−1=Aek−1+wk−1(21)\begin{aligned} e_{k}^{-} &=x_{k}-\hat{x}_{k}^{-} \\ &=A x_{k-1}+B u_{k-1}+w_{k-1}-A \hat{x}_{k-1}-B u_{k-1} \\ &=A\left(x_{k-1}-\hat{x}_{k-1}\right)+w_{k-1} \\ &=A e_{k-1}+w_{k-1}\tag{21} \end{aligned}

将上式代入式（20）：

Pk−=E[(Aek−1+wk−1)(ek−1⊤A⊤+wk−1⊤)]=E(Aek−1ek−1⊤A⊤)+E(wk−1wk−1⊤)=AE(ek−1ek−1⊤)A⊤+E(wk−1wk−1⊤)=APk−1A⊤+Q(22)\begin{aligned} P_{k}^{-} &=E\left[\left(A e_{k-1}+w_{k-1}\right)\left(e_{k-1}^{\top} A^{\top}+w_{k-1}^{\top}\right)\right] \\ &=E\left(A e_{k-1} e_{k-1}^{\top} A^{\top}\right)+E\left(w_{k-1} w_{k-1}^{\top}\right) \\ &=A E\left(e_{k-1} e_{k-1}^{\top}\right) A^{\top}+E\left(w_{k-1} w_{k-1}^{\top}\right) \\ &=A P_{k-1} A^{\top}+Q \tag{22} \end{aligned}

式（22）给出了误差协方差矩阵 PkP_k 的递推计算方法，根据上一时刻的误差协方差矩阵 Pk−1P_{k-1} 和过程噪声协方差矩阵 QQ 来计算。

那么至此，我们就能够得到卡尔曼滤波器的工作步骤了：

  1. 根据模型计算先验估计值：x^k−=Ax^k−1+Buk−1\hat{x}_{k}^{-}=A \hat{x}_{k-1}+B u_{k-1}.
  2. 计算先验误差协方差矩阵：Pk−=APk−1A⊤+QP_{k}^{-}=A P_{k-1} A^{\top}+Q.
  3. 计算卡尔曼增益：Kk=Pk−H⊤HPk−H⊤+RK_{k}=\frac{P_{k}^{-} H^{\top}}{H P_{k}^{-} H^{\top}+R}
  4. 得到最终估计值（后验估计）：x^k=x^k−+Kk(zk−Hx^k−)\hat{x}_{k}=\hat{x}_{k}^{-}+K_{k}\left(z_{k}-H \hat{x}_{k}^{-}\right)
  5. 更新误差协方差矩阵：Pk=(I−KkH)Pk−P_k=(I-K_kH)P_k^{-}

其中第5步更新 PkP_k 用于下一时刻计算 Pk−P_{k}^{-} 。由于卡尔曼滤波器是不断递推工作的，所以第一次需要给 x^k−1\hat{x}_{k-1} 和 Pk−1P_{k-1} 赋初值。

参考文献

  1. DR_CAN的精彩讲解