相机标定和相关坐标转换

引言

最近做一门课的课程作业，目标是实现目标的识别和定位，并控制机械臂对目标进行抓取，老师提供的是淘宝买到的学习套件。在实现目标识别功能的过程中，涉及到对相机进行标定、并将像素坐标系下的物体坐标转换为世界坐标系下的坐标。对于这部分内容，我参考了很多网上的文章，这里对整个学习过程进行一个梳理记录。

相机标定

针孔相机模型

普通相机成像可以采用小孔成像模型，将像平面镜像对称至物体同侧便于分析坐标的对应关系：

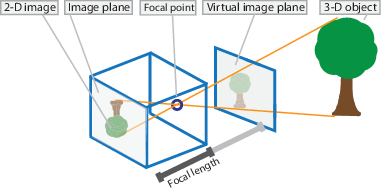
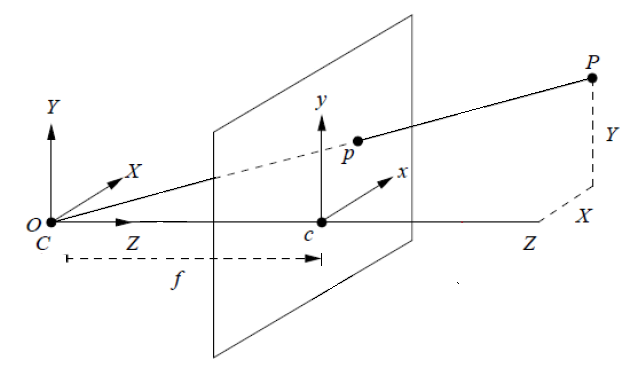
对于成像物体上的点P，其在像平面上对应点p，根据相似三角形，它们之间的坐标对应关系有：

$$\frac{f}{Z}=\frac{x}{X}=\frac{y}{Y}$$

有相机坐标系与图像坐标系的关系为：

$$Z_{c}\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{lll} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X_{c} \\ Y_{c} \\ Z_{c} \end{array}\right]$$

式中：$(x,y)$为图像坐标系像素点坐标，$(X_c, Y_c, Z_c)$为相机坐标系下物体点坐标。

图像坐标系和像素坐标系的关系

上面得到了图像坐标系和相机坐标系的关系，我们实际对图像进行分析的时候，多是使用像素坐标系，两者之间的关系如下：

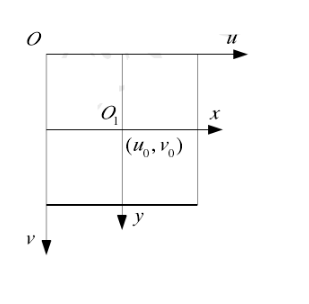
两者之间实际上还存在一个平移和比例缩放关系，像素坐标系单位是像素值pixel，而图像坐标系单位是长度单位mm或m。

图像坐标系（图中的 $[O_1, x, y]$ 坐标系）和像素坐标系（图中的 $[O, u, v]$ 坐标系）中坐标的关系如下：

$$\left\{\begin{array}{l} u=\frac{x}{d x}+u_{0} \\ v=\frac{y}{d y}+v_{0} \end{array}\right.$$

式中：$u,v$ 为像素坐标系下的坐标，单位为pixel，$dx,dy$ 分别是不同方向上的伸缩比例，单位为mm/pixel或m/pixel，$u_0,v_0$分别为主点偏移量，即图像坐标系相对于像素坐标系的偏移，单位也是pixel。

将这个公式和上述相机坐标系和图像坐标系关系的公式联合起来，可以得到相机坐标系和像素坐标系之间的关系：

$$Z_c \left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} \frac{1}{d x} & 0 & u_{0} \\ 0 & \frac{1}{d y} & v_{0} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X_c \\ Y_c \\ Z_c \end{array}\right]$$

上述结果是假定图像传感器原件两轴相互垂直，实际过程中可能会存在歪斜：

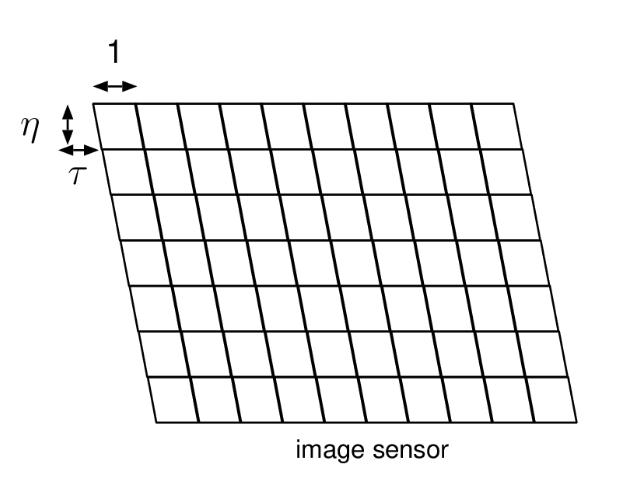
这时上述公式变为：

$$Z_c \left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_u & s & u_{0} \\ 0 & f_v & v_{0} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X_c \\ Y_c \\ Z_c \end{array}\right]$$

注意，上式中修改了部分变量的表示方法，为了使矩阵更好看。

世界坐标系和相机坐标系的关系

我们现在得到了图像像素坐标和物体点在相机坐标系下的坐标，但是实际情况是，我们的相机安装在机械臂上(眼在手上)或者安装在机械臂外的某一固定位置(眼在手外)。

机械臂能够直接利用的物体坐标是相对于机械臂坐标系的，这里我们称为基坐标系或世界坐标系。因此我们要解决的问题是如何得到世界坐标系和相机坐标系的关系。

实际上，任何两个三维坐标系之间的关系都可以用旋转加平移来得到。

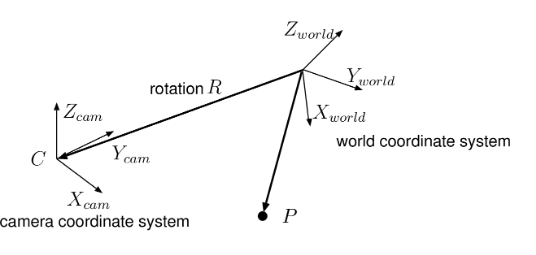
从世界坐标系坐标 $X_{world}$ 转换至相机坐标系坐标 $X_{cam}$ 的过程如下：

1. 首先绕Z轴旋转一个偏航角 $\psi$ ，相应的旋转矩阵为：

$$\mathbf{R_{z}}=\left[\begin{array}{ccc} \cos (\psi) & -\sin (\psi) & 0 \\ \sin (\psi) & \cos (\psi) & 0 \\ 0 & 0 & 1 \end{array}\right]$$

2. 然后绕Y轴旋转一个俯仰角 $\theta$ ，相应的旋转矩阵为：

$$\mathbf{R_{y}}=\left[\begin{array}{ccc} \cos (\theta) & 0 & \sin (\theta) \\ 0 & 1 & 0 \\ -\sin (\theta ) & 0 & \cos (\theta) \end{array}\right]$$

3. 最后绕X轴旋转一个滚转角 $\phi$ ，相应的旋转矩阵为：

$$\mathbf{R_{x}}=\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos (\phi) & -\sin (\phi) \\ 0 & \sin (\phi) & \cos (\phi) \end{array}\right]$$

4. 经过三次旋转之后，两个坐标系之间就只差一个平移量，这个平移量为相机坐标系原点在世界坐标系下的坐标，记作 $\mathbf{T}$ 。

因此，最终的转换关系为：

$$X_{cam} = \mathbf{R_{x}}\mathbf{R_{y}}\mathbf{R_{z}}X_{world} + \mathbf{T}$$

即将某个点在相机坐标系下的坐标 $X_{cam}$ 为 其在世界坐标系下坐标 $X_{world}$ 经过三次旋转加一次平移得到。

这里将上述旋转矩阵记为:

$$\mathbf{R_{3\times3}} = \mathbf{R_{x}}\mathbf{R_{y}}\mathbf{R_{z}}$$

$$\mathbf{T_{3 \times 1}} = \mathbf{T}$$

并增加坐标维数实现旋转和平移的统一：

$$\left[\begin{array}{c} X_{c} \\ Y_{c} \\ Z_{c} \\ 1 \end{array}\right]=\left[\begin{array}{cc} \mathbf{R_{3\times3}} & \mathbf{T_{3 \times 1}} \\ O & 1 \end{array}\right] \cdot\left[\begin{array}{c} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{array}\right]$$

其中 $X_c, Y_c, Z_c$ 为相机坐标系下坐标，$X_w, Y_w, Z_w$ 为世界坐标系下坐标。最后联合上面推到的像素坐标系和相机坐标系的关系，能够得到像素坐标系和世界坐标系之间的关系：

$$Z_{c}\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{cccc} f_{u} & s & u_{0} & 0 \\ 0 & f_{v} & v_{0} & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{cc} \mathbf{R_{3\times3}} & \mathbf{T_{3 \times 1}} \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{array}\right]$$

上式就是我们得到的最终的像素坐标系和世界坐标系之间的转换关系，我们记上式为：

$$Z_{c}\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]=\left[\mathbf{K}, \mathbf{0}_{3}\right]\cdot\mathbf{N}\cdot\left[\begin{array}{c} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{array}\right]$$

其中：$\mathbf{K}$ 是相机的内参矩阵，只和相机的焦距、成像单元歪斜程度等内部参数有关，一般而言相机的内参在出厂时就已经确定；$\mathbf{N}$ 是相机的外参矩阵，它描述了相机坐标系和世界坐标系之间的旋转和平移关系。

Matlab相机标定工具箱

为了确定相机的内参和外参，可以使用Matlab标定工具箱或者Opencv图像处理库或者Ros中的相应标定包进行。我这里使用Matlab相机标定工具箱，具体的参数标定原理，这里不打算详细介绍，给出一个相关的介绍链接：https://zhuanlan.zhihu.com/p/94244568。

首先需要准备相机标定专用的棋盘格图片，将其贴在一个平面上(标定平面)，使用待标定相机拍摄不同方向上的若干照片，一般以15张至20张为宜，标定工具箱会自动提取出棋盘格角点，进行相机内参、外参以及畸变参数的估计。

最终标定结果如下：

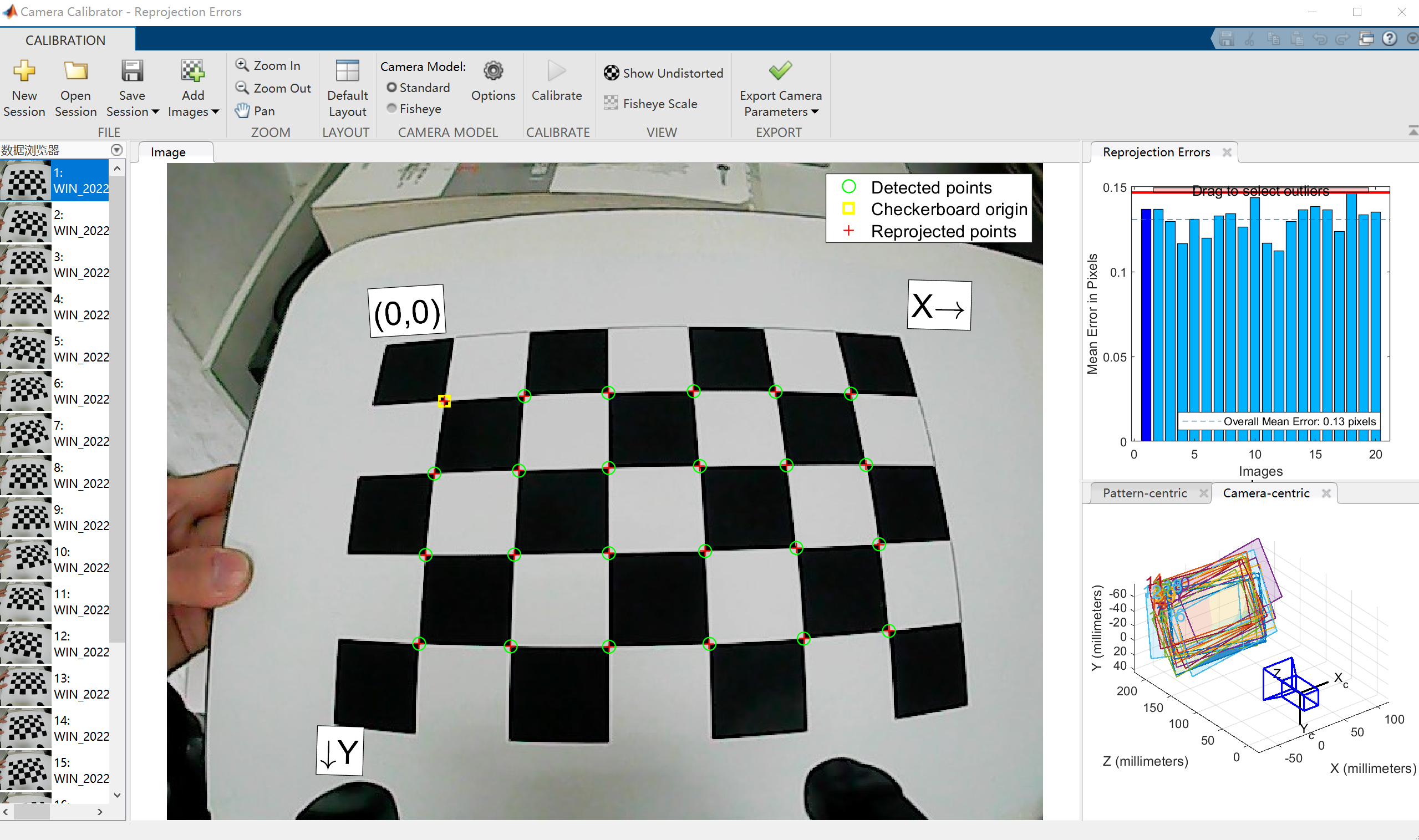
点击导出相机参数，能够获得相机的若干参数：

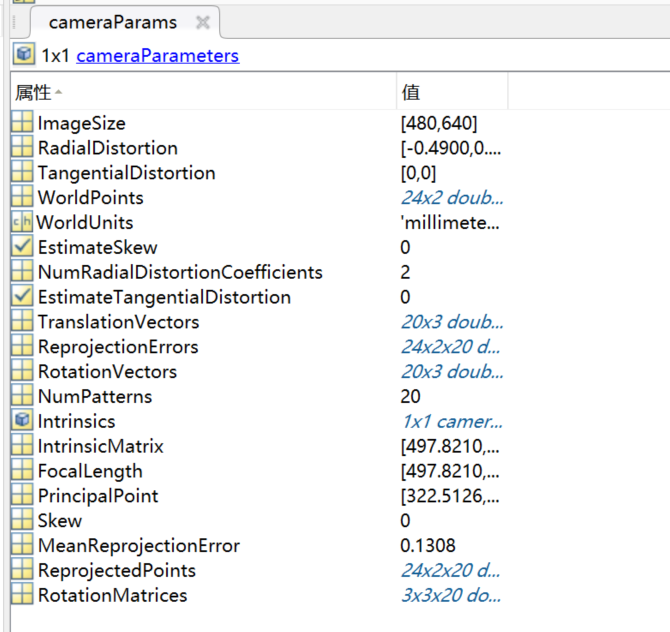
需要特别关注的几个参数有：

1. 相机的内参矩阵 cameraParams.IntrinsicMatrix，这是一个$3\times3$的矩阵。
2. 相机的畸变参数 cameraParams.RadialDistortion和cameraParams.TangentialDistortion。
3. 相机的外参矩阵，对于每张标定图片都有一个外参矩阵，上面说过外参矩阵用一个旋转矩阵和一个平移向量描述了相机坐标系和世界坐标系之间的转换关系。这里的世界坐标系是以标定板第一个检测出角点为原点，标定板平面为XY平面的坐标系。每张标定图片的棋盘格位置不同，因此外参矩阵也不同。外参矩阵的旋转矩阵为：cameraParams.RotationMatrices，平移向量为：cameraParams.TranslationVectors。

目标定位和坐标转换

在此次作业中，我的方案是通过二维码识别物体所在位置，并将其传给机械臂用于逆运动学解算从而实现抓取。这里首先面临的问题就是如何从物体的像素坐标得到物体在机械臂基坐标系下的坐标。

实际上，我们可以通过相机的内参从物体的像素坐标得到物体在相机坐标系下的坐标，通过外参矩阵得到物体在标定板世界坐标系的坐标。如果将标定板放置在机械臂基坐标系平面内，标定板世界坐标系和机械臂坐标系之间的转换关系就较为简单。

下面着重推导一下如何根据像素坐标求得世界坐标：

$$Z_{c}\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{cccc} f_{u} & s & u_{0} \\ 0 & f_{v} & v_{0} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cc} \mathbf{R_{3\times3}} & \mathbf{T_{3 \times 1}} \end{array}\right]\left[\begin{array}{c} X_{w} \\ Y_{w} \\ Z_{w} \end{array}\right]$$

若已知内参矩阵和外参矩阵，还有一个伸缩因子 $Z_c$ 是未知的，实际上，我们把标定板上的点的 $Z_w$ 都取为0，这个伸缩因子是可以求出来的。

对上式等式左右分别左乘内参矩阵的逆 $\mathbf{K}^{-1}$ 和旋转矩阵的逆 $\mathbf{R_{3\times3}^{-1}}$：

$$\left[\begin{array}{lll} a 11 & \text { a12 } & a 13 \\ a 21 & a 22 & a 23 \\ a 31 & a 32 & a 33 \end{array}\right] Z_c\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\left[\begin{array}{c} X w \\ Y w \\ Z w \end{array}\right]+\left[\begin{array}{l} b 11 \\ b 12 \\ b 13 \end{array}\right]$$

由于内参矩阵和外参矩阵通过标定获得，上式中所有 $a_{ij}$ 和 $b_{ij}$ 都是已知的，取 $Z_w=0$ 能够求出伸缩因子，从而求出像素坐标为 $(u, v)$ 的像素点对应的世界坐标系下的坐标。

下面是程序实现(这里使用Python版的Opencv实现)：

# 相机内参
intrinsicMatrix = np.array([[497.821047687599, 0, 322.512606213576], [0, 496.039066791915, 253.965957147879], [0, 0, 1]])

# 相机外参(某一张标定板照片对应)
# 旋转矩阵
rotation_matrix = np.array([[0.9988, -0.0217, -0.0446], [0.0018, 0.9140, -0.4056], [0.0496, 0.4051, 0.9129]])
trans_vector = np.array([-51.6844018784524,-34.6647774948010,206.755333272538]).reshape(3, 1)

def cameraToWorld(intrinsic_matrix, r, t, img_point):
    ''' 
    通过相机内外参求取伸缩因子，并从像素坐标求取世界坐标系下的位置(相对于标定板角点)
    @param intrinsic_matrix 相机内参
    @param r 相机外参旋转矩阵
    @param t 相机外参平移向量
    @param img_point 像素坐标系坐标
    '''
    print("intrinsic_matrix:\n", intrinsic_matrix, end='\n\n')
    print("rotation_matrix:\n", r, end='\n\n')
    print("trans_vector:\n", t, end='\n\n')
    Zw = 0
    # 像素坐标矩阵
    img_point = np.array([img_point[0], img_point[1], 1]).reshape(3,1)
    # 矩阵乘法
    left_side = np.linalg.inv(r) @ np.linalg.inv(intrinsic_matrix) @ img_point
    right_side = np.linalg.inv(r) @ t
    s = Zw + right_side[2][0] / left_side[2][0]
    print("s:", s)
    worldPoint = left_side * s - right_side
    return [worldPoint[0][0], worldPoint[1][0]]

参考文献

1. https://zhuanlan.zhihu.com/p/87334006
2. https://blog.csdn.net/qq_42422098/article/details/108473493
3. https://zhuanlan.zhihu.com/p/94244568